Naada Harmonica

A harmonica is a small, rectangular musical instrument with a series of metal reeds attached to individual chambers. It is played by using the mouth to create air-streams that pass through the reeds, causing them to vibrate and produce sound. The harmonica is often referred to as a “free reed” instrument because the reeds can vibrate freely when air passes through them.

Articulations and Playing options

Naada Harmonica supports:

  • Tremolo
  • Vibrato
  • Bends
  • Mute (wah-wah)
  • Mono/Polyphony

Physics

Figure 1: Type of reeds on a Harmonica

A Harmonica typically has two kinds of reeds based on how they are riveted (see Figure 1). A draw reed get activated when the player plays a note by drawing in air in contrast to a blow reed that gets activated when a note is played by blowing into the Harmonica.

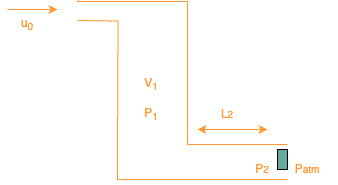
Figure 2: Model of the Mouth reservoir coupled with the reed for simulation

The reed oscillates close to it’s natural frequency because of the instability caused by it’s coupling with the mouth cavity acting as a resonator. We model this coupling as shown in Figure 2. This model of the coupled free reed is inspired from the work of Laurent Millot [1]. The reed (shown as a green block) is modeled as a spring driven by the force acting on an area Sr because of the difference in pressure across it’s two sides. The pressure on the inside is denoted P2 and the atmospheric pressure on the outside is denoted Patm. It should be noted that the effective area needed to compute the force changes with time based on the shape of the reed. The input flow of air is denoted to have a flow equal to u0. This air flow then enters a reservoir having volume V1 at pressure P1. Finally, the airflow acts on the reed after traveling a distance of L2 through a pipe with cross section area S2. This entire phenomenon is governed by the following five equations.

  • Mass conservation for the volume V1 :
\[ \frac{V_1}{c^2} \frac{d(P_1 – P_{atm})}{dt} = \rho_0 (u_0 – u) \], where u is the outgoing air flow, \(\rho_0\) and \(c\) are air density and speed of sound respectively.
  • Newton’s second law at the pipe of length L2:
\[ P_1 = P_2 + \rho_0 \frac{L_2}{S_2} \frac{du}{dt} \]
  • Bernoulli’s equation (a form of energy conservation) considering the outgoing air velocity vj :
\[P_2 = P_{atm} + \frac{1}{2} \rho_0 v_j^2 \]
  • Reed motion (driven spring) with Q, mass M and natural frequency ω0 :
\[\frac{d^2\tau}{dt^2} + Q^{-1}\omega_0 \frac{d\tau}{dt} + \omega_0^2\tau = \frac{S_r}{M}(P_2 – P_{atm})\]
  • Total output flow equation as a sum of the pump flow due to reed motion and the air going out :
\[u=S_r \frac{d\tau}{dt} + \alpha S_u v_j \], where \(S_u\) is the “useful section” or the area through which air escapes. \(\alpha\) is the vena contracta coefficient which typically takes the value of 0.611. The area of the section for air outflow is larger than the area of the jet itself. This is accounted for by using the factor \(\alpha\)

Naada Implementation

The set of five equations needs to be solved simultaneously at the sampling rate. By a series of back-substitutions, it is easy to see that the main part of the solution is in finding the root of a non linear equation. This is solved using an iterative technique until convergence is achieved. A python implementation of the reed simulation is available here. The interested reader is encouraged to play with it. The Naada implementation follows the Python prototype but is heavily optimized with SIMD instructions for performance. Though the mouth resonator model seems to be a simple one compared to others described in literature, it produces remarkably good results and matches the actual pressure waveform that originates from a real Harmonica very well.

Articulations and Dynamics

The harmonica is recognized for the different dynamics that are possible. The Naada implementation supports cupping/muting (Wah wah), flutter, modulation, polyphony (chords), expression (blow velocity), and pitch bending. All these are integrated in an intuitive way into the algorithm. The expression can change the frequency very slightly (< 1 Hz) like in a real harmonica. Further, realism is enhanced by automatic randomization of the blow velocity. Naada also takes the advantage of a software implementation not being limited by actual physics . On a real harmonica, the mouth cavity (volume V1 in our model) is adjusted to get a pitch bend but this is accomplished in Naada in a different way that ensures a bend of up-to two semitones in both directions. It is also possible to pitch bend a chord! This doesn’t affect the timbre of the sound but the purist needs to be careful about playing unrealistic phrases.

Note Range

The implementation supports a range of 2 and a half octaves starting from C4 (261 Hz, 440Hz tuning). The tuning can be altered by upto 30 cents in either directions. The default tuning is set to 440Hz.

References

  • [1] “A Proposal for a Minimal Model of Free Reeds“, Laurent Millot, Acta Acustica, January 2007,
  • [2] “The Physics of Musical Instruments“, Neville Fletcher, Thomas Rossing, Springer-Verlag, 1991